E2 Proposition 8 Scolie

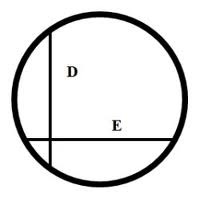
Si quelqu’un, pour une plus ample explication de cette chose, ressent le besoin d’un exemple, je n’en pourrai certes donner aucun qui explique adéquatement la chose dont je parle ici, vu qu’elle est unique ; j’essaierai pourtant d’illustrer la chose autant que faire se peut : un cercle est, on le sait, de nature telle que de toutes les lignes droites qui en lui se coupent en un même point, les rectangles faits sous leurs segments sont égaux entre eux; et donc, dans un cercle sont contenues une infinité de rectangles égaux entre eux ; et pourtant aucun d’entre eux ne peut être dite exister sinon en tant que le cercle existe, et l’idée non plus d’un quelconque de ces rectangles ne peut être dite exister, si ce n’est en tant qu’elle est comprise dans l’idée du cercle. Concevons cependant que de cette infinité de paires deux seulement existent, savoir D et E. Alors à coup sûr leurs idées aussi existent non pas seulement en tant qu’elles sont seulement incluse dans l’idée du cercle, mais aussi en tant qu’elles enveloppent l’existence de ces rectangles, ce qui fait qu’elles se distinguent des autres idées des autres rectangles.

Texte latin

Si quis ad uberiorem hujus rei explicationem exemplum desideret, nullum sane dare potero quod rem de qua hic loquor, utpote unicam adæquate explicet; conabor tamen rem ut fieri potest, illustrare. Nempe circulus talis est naturæ ut omnium linearum rectarum in eodem sese invicem secantium rectangula sub segmentis sint inter se æqualia; quare in circulo infinita inter se æqualia rectangula continentur : attamen nullum eorum potest dici existere nisi quatenus circulus existit nec etiam alicujus horum rectangulorum idea potest dici existere nisi quatenus in circuli idea comprehenditur. Concipiantur jam ex infinitis illis duo tantum nempe E et D existere. Sane eorum etiam ideæ jam non tantum existunt quatenus solummodo in circuli idea comprehenduntur sed etiam quatenus illorum rectangulorum existentiam involvunt, quo fit ut a reliquis reliquorum rectangulorum ideis distinguantur.​